97 Population Evolution

Learning Objectives

By the end of this section, you will be able to do the following:

  • Define population genetics and describe how scientists use population genetics in studying population evolution
  • Define the Hardy-Weinberg principle and discuss its importance

People did not understand the mechanisms of inheritance, or genetics, at the time Charles Darwin and Alfred Russel Wallace were developing their idea of natural selection. This lack of knowledge was a stumbling block to understanding many aspects of evolution. The predominant (and incorrect) genetic theory of the time, blending inheritance, made it difficult to understand how natural selection might operate. Darwin and Wallace were unaware of the Austrian monk Gregor Mendel’s 1866 publication “Experiments in Plant Hybridization”, which came out not long after Darwin’s book, On the Origin of Species. Scholars rediscovered Mendel’s work in the early twentieth century at which time geneticists were rapidly coming to an understanding of the basics of inheritance. Initially, the newly discovered particulate nature of genes made it difficult for biologists to understand how gradual evolution could occur. However, over the next few decades scientists integrated genetics and evolution in what became known as the modern synthesis—the coherent understanding of the relationship between natural selection and genetics that took shape by the 1940s. Generally, this concept is generally accepted today. In short, the modern synthesis describes how evolutionary processes, such as natural selection, can affect a population’s genetic makeup, and, in turn, how this can result in the gradual evolution of populations and species. The theory also connects population change over time (microevolution), with the processes that gave rise to new species and higher taxonomic groups with widely divergent characters, called (macroevolution).

Everyday Connection

Evolution and Flu VaccinesEvery fall, the media starts reporting on flu vaccinations and potential outbreaks. Scientists, health experts, and institutions determine recommendations for different parts of the population, predict optimal production and inoculation schedules, create vaccines, and set up clinics to provide inoculations. You may think of the annual flu shot as media hype, an important health protection, or just a briefly uncomfortable prick in your arm. However, do you think of it in terms of evolution?

The media hype of annual flu shots is scientifically grounded in our understanding of evolution. Each year, scientists across the globe strive to predict the flu strains that they anticipate as most widespread and harmful in the coming year. They base this knowledge on how flu strains have evolved over time and over the past few flu seasons. Scientists then work to create the most effective vaccine to combat those selected strains. Pharmaceutical companies produce hundreds of millions of doses in a short period in order to provide vaccinations to key populations at the optimal time.

Because viruses, like the flu, evolve very quickly (especially in evolutionary time), this poses quite a challenge. Viruses mutate and replicate at a fast rate, so the vaccine developed to protect against last year’s flu strain may not provide the protection one needs against the coming year’s strain. Evolution of these viruses means continued adaptions to ensure survival, including adaptations to survive previous vaccines.

Population Genetics

Recall that a gene for a particular character may have several alleles, or variants, that code for different traits associated with that character. For example, in the ABO blood type system in humans, three alleles determine the particular blood-type carbohydrate on the surface of red blood cells. Each individual in a population of diploid organisms can only carry two alleles for a particular gene, but more than two may be present in the individuals that comprise the population. Mendel followed alleles as they were inherited from parent to offspring. In the early twentieth century, biologists in the area of population genetics began to study how selective forces change a population through changes in allele and genotypic frequencies.

The allele frequency (or gene frequency) is the rate at which a specific allele appears within a population. Until now we have discussed evolution as a change in the characteristics of a population of organisms, but behind that phenotypic change is genetic change. In population genetics, scientists define the term evolution as a change in the allele’s frequency in a population. Using the ABO blood type system as an example, the frequency of one of the alleles, IA, is the number of copies of that allele divided by all the copies of the ABO gene in the population. For example, a study in Jordan1 found a frequency of IA to be 26.1 percent. The IB and I0 alleles comprise 13.4 percent and 60.5 percent of the alleles respectively, and all of the frequencies added up to 100 percent. A change in this frequency over time would constitute evolution in the population.

The allele frequency within a given population can change depending on environmental factors; therefore, certain alleles become more widespread than others during the natural selection process. Natural selection can alter the population’s genetic makeup. An example is if a given allele confers a phenotype that allows an individual to better survive or have more offspring. Because many of those offspring will also carry the beneficial allele, and often the corresponding phenotype, they will have more offspring of their own that also carry the allele, thus, perpetuating the cycle. Over time, the allele will spread throughout the population. Some alleles will quickly become fixed in this way, meaning that every individual of the population will carry the allele, while detrimental mutations may be swiftly eliminated if derived from a dominant allele from the gene pool. The gene pool is the sum of all the alleles in a population.

Sometimes, allele frequencies within a population change randomly with no advantage to the population over existing allele frequencies. We call this phenomenon genetic drift. Natural selection and genetic drift usually occur simultaneously in populations and are not isolated events. It is hard to determine which process dominates because it is often nearly impossible to determine the cause of change in allele frequencies at each occurrence. We call an event that initiates an allele frequency change in an isolated part of the population, which is not typical of the original population, the founder effect. Natural selection, random drift, and founder effects can lead to significant changes in a population’s genome.

Hardy-Weinberg Principle of Equilibrium

In the early twentieth century, English mathematician Godfrey Hardy and German physician Wilhelm Weinberg stated the principle of equilibrium to describe the population’s genetic makeup. The theory, which later became known as the Hardy-Weinberg principle of equilibrium, states that a population’s allele and genotype frequencies are inherently stable— unless some kind of evolutionary force is acting upon the population, neither the allele nor the genotypic frequencies would change. The Hardy-Weinberg principle assumes conditions with no mutations, migration, emigration, or selective pressure for or against genotype, plus an infinite population. While no population can satisfy those conditions, the principle offers a useful model against which to compare real population changes.

Working under this theory, population geneticists represent different alleles as different variables in their mathematical models. The variable p, for example, often represents the frequency of a particular allele, say Y for the trait of yellow in Mendel’s peas, while the variable q represents the frequency of y alleles that confer the color green. If these are the only two possible alleles for a given locus in the population, p + q = 1. In other words, all the p alleles and all the q alleles comprise all of the alleles for that locus in the population.

However, what ultimately interests most biologists is not the frequencies of different alleles, but the frequencies of the resulting genotypes, known as the population’s genetic structure, from which scientists can surmise phenotype distribution. If we observe the phenotype, we can know only the homozygous recessive allele’s genotype. The calculations provide an estimate of the remaining genotypes. Since each individual carries two alleles per gene, if we know the allele frequencies (p and q), predicting the genotypes’ frequencies is a simple mathematical calculation to determine the probability of obtaining these genotypes if we draw two alleles at random from the gene pool. In the above scenario, an individual pea plant could be pp (YY), and thus produce yellow peas; pq (Yy), also yellow; or qq (yy), and thus produce green peas ((Figure)). In other words, the frequency of pp individuals is simply p2; the frequency of pq individuals is 2pq; and the frequency of qq individuals is q2. Again, if p and q are the only two possible alleles for a given trait in the population, these genotypes frequencies will sum to one: p2 + 2pq + q2 = 1.

Visual Connection
When populations are in the Hardy-Weinberg equilibrium, the allelic frequency is stable from generation to generation and we can determine the allele distribution from the Hardy-Weinberg equation. If the allelic frequency measured in the field differs from the predicted value, scientists can make inferences about what evolutionary forces are at play.


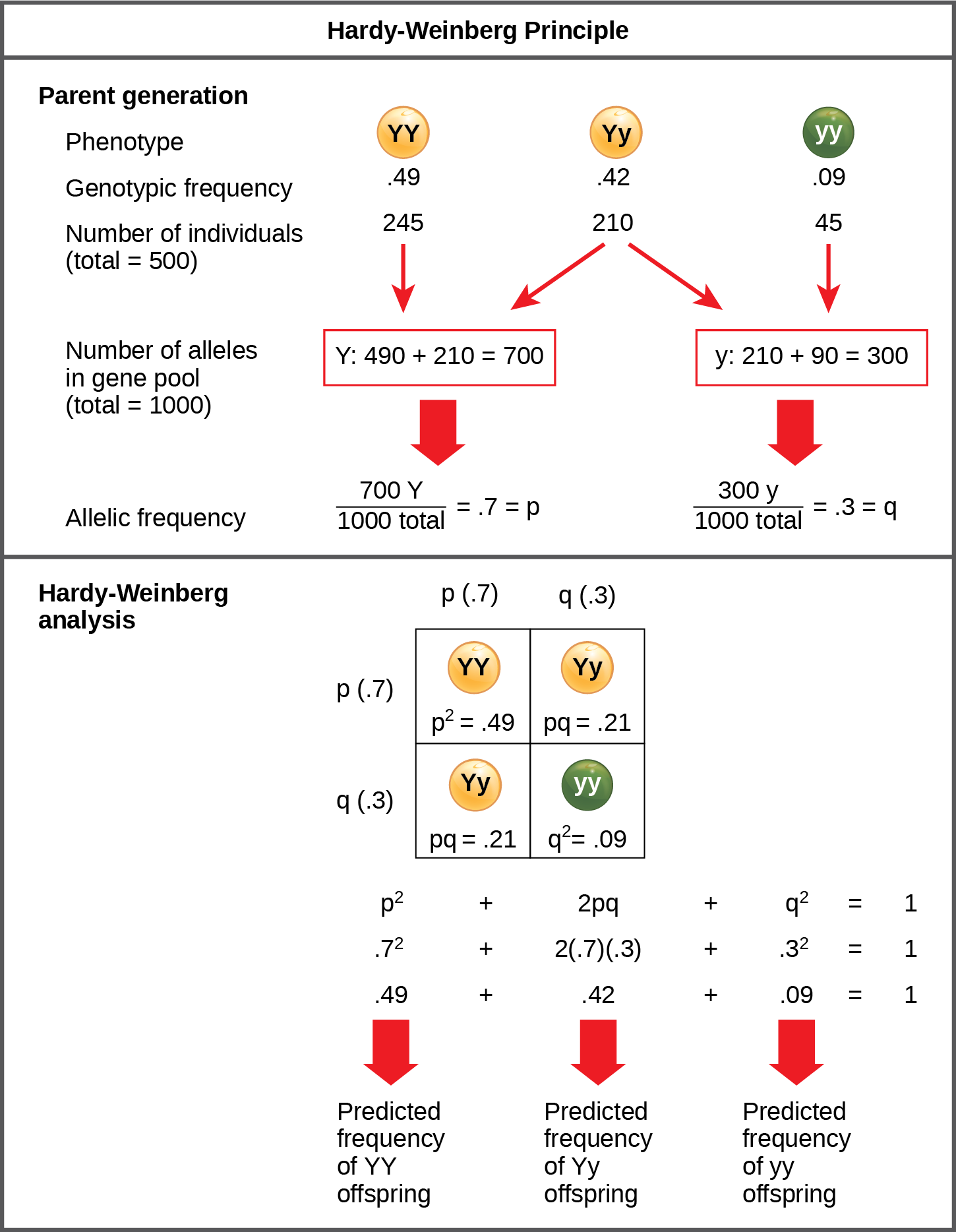
The Hardy-Weinberg principle is used to predict the genotypic distribution of offspring in a given population. In the example given, pea plants have two different alleles for pea color. The dominant capital Y allele results in yellow pea color, and the recessive small y allele results in green pea color. The distribution of individuals in a population of 500 is given. Of the 500 individuals, 245 are homozygous dominant (capital Y capital Y) and produce yellow peas. 210 are heterozygous (capital Y small y) and also produce yellow peas. 45 are homozygous recessive (small y small y) and produce green peas. The frequencies of homozygous dominant, heterozygous, and homozygous recessive individuals are 0.49, 0.42, and 0.09, respectively. Each of the 500 individuals provides two alleles to the gene pool, or 1000 total. The 245 homozygous dominant individuals provide two capital Y alleles to the gene pool, or 490 total. The 210 heterozygous individuals provide 210 capital Y and 210 small y alleles to the gene pool. The 45 homozygous recessive individuals provide two small y alleles to the gene pool, or 90 total. The number of capital Y alleles is 490 from homozygous dominant individuals plus 210 from homozygous recessive individuals, or 700 total. The number of small y alleles is 210 from heterozygous individuals plus 90 from homozygous recessive individuals, or 300 total. The allelic frequency is calculated by dividing the number of each allele by the total number of alleles in the gene pool. For the capital Y allele, the allelic frequency is 700 divided by 1000, or 0.7; this allelic frequency is called p. For the small y allele the allelic frequency is 300 divided by 1000, or 0.3; the allelic frequency is called q. Hardy-Weinberg analysis is used to determine the genotypic frequency in the offspring. The Hardy-Wienberg equation is p-squared plus 2pq plus q-squared equals 1. For the population given, the frequency is 0.7-squared plus 2 times .7 times .3 plus .3-squared equals one. The value for p-squared, 0.49, is the predicted frequency of homozygous dominant (capital Y capital Y) individuals. The value for 2pq, 0.42, is the predicted frequency of heterozygous (capital Y small y) individuals. The value for q-squared, .09, is the predicted frequency of homozygous recessive individuals. Note that the predicted frequency of genotypes in the offspring is the same as the frequency of genotypes in the parent population. If all the genotypic frequencies, .49 plus .42 plus .09, are added together, the result is one

In plants, violet flower color (V) is dominant over white (v). If p = 0.8 and q = 0.2 in a population of 500 plants, how many individuals would you expect to be homozygous dominant (VV), heterozygous (Vv), and homozygous recessive (vv)? How many plants would you expect to have violet flowers, and how many would have white flowers?

<!–<para>The expected distribution is 320 VV, 160Vv, and 20 vv plants. Plants with VV or Vv genotypes would have violet flowers, and plants with the vv genotype would have white flowers, so a total of 480 plants would be expected to have violet flowers, and 20 plants would have white flowers.–>

In theory, if a population is at equilibrium—that is, there are no evolutionary forces acting upon it—generation after generation would have the same gene pool and genetic structure, and these equations would all hold true all of the time. Of course, even Hardy and Weinberg recognized that no natural population is immune to evolution. Populations in nature are constantly changing in genetic makeup due to drift, mutation, possibly migration, and selection. As a result, the only way to determine the exact distribution of phenotypes in a population is to go out and count them. However, the Hardy-Weinberg principle gives scientists a mathematical baseline of a non-evolving population to which they can compare evolving populations and thereby infer what evolutionary forces might be at play. If the frequencies of alleles or genotypes deviate from the value expected from the Hardy-Weinberg equation, then the population is evolving.

Link to Learning

Use this online calculator to determine a population’s genetic structure.

Section Summary

The modern synthesis of evolutionary theory grew out of the cohesion of Darwin’s, Wallace’s, and Mendel’s thoughts on evolution and heredity, along with the more modern study of population genetics. It describes the evolution of populations and species, from small-scale changes among individuals to large-scale changes over paleontological time periods. To understand how organisms evolve, scientists can track populations’ allele frequencies over time. If they differ from generation to generation, scientists can conclude that the population is not in Hardy-Weinberg equilibrium, and is thus evolving.

Visual Connection Questions

(Figure) In plants, violet flower color (V) is dominant over white (v). If p = .8 and q = 0.2 in a population of 500 plants, how many individuals would you expect to be homozygous dominant (VV), heterozygous (Vv), and homozygous recessive (vv)? How many plants would you expect to have violet flowers, and how many would have white flowers?

(Figure) The expected distribution is 320 VV, 160Vv, and 20 vv plants. Plants with VV or Vv genotypes would have violet flowers, and plants with the vv genotype would have white flowers, so a total of 480 plants would be expected to have violet flowers, and 20 plants would have white flowers.

Review Questions

What is the difference between micro- and macroevolution?

  1. Microevolution describes the evolution of small organisms, such as insects, while macroevolution describes the evolution of large organisms, like people and elephants.
  2. Microevolution describes the evolution of microscopic entities, such as molecules and proteins, while macroevolution describes the evolution of whole organisms.
  3. Microevolution describes the evolution of organisms in populations, while macroevolution describes the evolution of species over long periods of time.
  4. Microevolution describes the evolution of organisms over their lifetimes, while macroevolution describes the evolution of organisms over multiple generations.

C

Population genetics is the study of:

  1. how selective forces change the allele frequencies in a population over time
  2. the genetic basis of population-wide traits
  3. whether traits have a genetic basis
  4. the degree of inbreeding in a population

A

Which of the following populations is not in Hardy-Weinberg equilibrium?

  1. a population with 12 homozygous recessive individuals (yy), 8 homozygous dominant individuals (YY), and 4 heterozygous individuals (Yy)
  2. a population in which the allele frequencies do not change over time
  3. p2 + 2pq + q2 = 1
  4. a population undergoing natural selection

D

One of the original Amish colonies rose from a ship of colonists that came from Europe. The ship’s captain, who had polydactyly, a rare dominant trait, was one of the original colonists. Today, we see a much higher frequency of polydactyly in the Amish population. This is an example of:

  1. natural selection
  2. genetic drift
  3. founder effect
  4. b and c

D

Critical Thinking Questions

Solve for the genetic structure of a population with 12 homozygous recessive individuals (yy), 8 homozygous dominant individuals (YY), and 4 heterozygous individuals (Yy).

p = (8*2 + 4)/48 = .42; q = (12*2 + 4)/48 = .58; p2 = .17; 2pq = .48; q2 = .34

Explain the Hardy-Weinberg principle of equilibrium theory.

The Hardy-Weinberg principle of equilibrium is used to describe the genetic makeup of a population. The theory states that a population’s allele and genotype frequencies are inherently stable: unless some kind of evolutionary force is acting upon the population, generation after generation of the population would carry the same genes, and individuals would, as a whole, look essentially the same.

Imagine you are trying to test whether a population of flowers is undergoing evolution. You suspect there is selection pressure on the color of the flower: bees seem to cluster around the red flowers more often than the blue flowers. In a separate experiment, you discover blue flower color is dominant to red flower color. In a field, you count 600 blue flowers and 200 red flowers. What would you expect the genetic structure of the flowers to be?

Red is recessive so q2 = 200/800 = 0.25; q = 0.5; p = 1 – q = 0.5; p2 = 0.25; 2pq = 0.5. You would expect 200 homozygous blue flowers, 400 heterozygous blue flowers, and 200 red flowers.

Footnotes

  • 1 Sahar S. Hanania, Dhia S. Hassawi, and Nidal M. Irshaid, “Allele Frequency and Molecular Genotypes of ABO Blood Group System in a Jordanian Population,” Journal of Medical Sciences 7 (2007): 51-58, doi:10.3923/jms.2007.51.58.

Glossary

allele frequency
(also, gene frequency) rate at which a specific allele appears within a population
founder effect
event that initiates an allele frequency change in part of the population, which is not typical of the original population
gene pool
all the alleles that the individuals in the population carry
genetic structure
distribution of the different possible genotypes in a population
macroevolution
broader scale evolutionary changes that scientists see over paleontological time
microevolution
changes in a population’s genetic structure
modern synthesis
overarching evolutionary paradigm that took shape by the 1940s and scientists generally accept today
population genetics
study of how selective forces change the allele frequencies in a population over time

License

Icon for the Creative Commons Attribution 4.0 International License

Biology 2e Copyright © 2018 by OpenStax Biology 2nd Edition is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book